Penjelasan Permainan Menara Hanoi

Daftar Isi

Sejarah Permainan Menara Hanoi

Sejarah permainan Tower of Hanoi berasal dari seorang matematikawan asal Perancis bernama Edouard Lucas pada tahun 1883. Lucas pertama kali memperkenalkan permainan ini sebagai sebuah teka-teki matematika yang dapat digunakan untuk menunjukkan prinsip rekursi dan untuk menunjukkan kompleksitas algoritma.

Permainan ini menjadi sangat populer di kalangan matematikawan dan ilmuwan komputer dan digunakan sebagai sebuah percontohan dalam bidang ilmu komputasi dan teori kompleksitas.

Selain itu, permainan ini juga digunakan sebagai sebuah tool dalam pembelajaran matematika di sekolah-sekolah dan perguruan tinggi, karena permainan ini dapat digunakan untuk menunjukkan konsep-konsep matematika seperti rekursi, logika dan pemecahan masalah.

Sampai saat ini, permainan ini masih populer di kalangan matematikawan, ilmuwan komputer, dan pembelajar matematika di seluruh dunia. Beberapa variasi dari permainan ini juga dikembangkan, seperti menara hanoi dengan lebih dari 3 tiang, menggunakan disk yang berbeda jumlah dan ukuran.

Pengertian Permainan Menara Hanoi

Tower of Hanoi adalah sebuah permainan matematika yang terdiri dari tiga tiang dan beberapa disk yang berbeda ukuran. Tujuan dari permainan ini adalah untuk memindahkan semua disk dari tiang awal ke tiang tujuan.

Secara umum, perhitungan matematika dalam Tower of Hanoi cukup sederhana dan dapat dijelaskan dengan menggunakan metode rekursi. Namun, meskipun perhitungan ini sederhana, permainan ini dapat menjadi sangat sulit untuk diselesaikan jika terdapat banyak disk yang harus dipindahkan.

Selain perhitungan matematika yang sederhana, Tower of Hanoi juga memiliki banyak aplikasi dalam bidang komputer dan ilmu komputasi. Salah satu aplikasinya adalah dalam algoritma pencarian. Beberapa algoritma pencarian seperti algoritma DFS (depth first search) dan BFS (breadth first search) dapat diterapkan dalam permainan Tower of Hanoi untuk menemukan solusi yang paling optimal.

Tower of Hanoi juga dapat digunakan dalam pemrograman rekursif. Beberapa bahasa pemrograman seperti C, C++, dan Python menyediakan fungsi rekursif yang dapat digunakan untuk menyelesaikan permainan ini. Dengan menggunakan pemrograman rekursif, kita dapat menuliskan kode yang sederhana dan mudah dipahami.

Tower of Hanoi dapat digunakan sebagai analogi untuk masalah yang lebih kompleks dalam ilmu komputasi, seperti masalah backtracking dan masalah optimasi. Contohnya, dalam problem backtracking seperti 8 queen problem, kita dapat menganggap setiap disk sebagai sebuah ratu dan setiap tiang sebagai sebuah bidak.

Aturan Permainan Menara Hanoi

Aturan permainan Tower of Hanoi cukup sederhana. Terdapat tiga tiang yang disebut tiang A, B, dan C. Pada tiang A, terdapat beberapa disk yang berbeda ukuran, yang ditempatkan dari yang terbesar di bawah hingga yang terkecil di atas. Tujuan dari permainan ini adalah untuk memindahkan semua disk dari tiang A ke tiang C, dengan syarat bahwa tidak boleh ada disk yang lebih besar yang berada di atas disk yang lebih kecil.

Beberapa aturan yang harus diikuti dalam permainan ini adalah:

1. Hanya satu disk dapat dipindahkan pada satu waktu.
2. Disk yang lebih besar tidak boleh diletakkan di atas disk yang lebih kecil.
3. Disk hanya boleh dipindahkan dari tiang ke tiang lain.

Pemain dapat memulai dengan memindahkan disk terkecil dari tiang A ke tiang B. Kemudian, pemain dapat memindahkan disk yang lebih besar dari tiang A ke tiang C. Setelah itu, pemain dapat memindahkan disk terkecil dari tiang B ke tiang C. Proses ini harus dilakukan secara berulang hingga semua disk berhasil dipindahkan dari tiang A ke tiang C.

Rumus Permainan Menara Hanoi

Rumus yang digunakan dalam permainan Tower of Hanoi adalah 2^n-1, dimana n adalah jumlah disk yang ada pada tiang A. Ini berarti bahwa jika terdapat n disk pada tiang A, maka jumlah langkah yang dibutuhkan untuk menyelesaikan permainan ini adalah 2^n-1.

Ini dapat dijelaskan dengan menggunakan metode rekursi. Secara umum, jika kita ingin memindahkan n disk dari tiang A ke tiang C, kita dapat memecah masalah ini menjadi dua masalah lebih kecil. Pertama, kita dapat memindahkan n-1 disk dari tiang A ke tiang B. Kedua, kita dapat memindahkan disk terakhir dari tiang A ke tiang C. Dan ketiga, kita dapat memindahkan n-1 disk dari tiang B ke tiang C.

Jika kita menggunakan metode rekursi untuk menyelesaikan masalah ini, maka setiap kali kita memecah masalah menjadi masalah lebih kecil, kita akan membutuhkan 2 langkah untuk setiap masalah lebih kecil. Dengan kata lain, jika kita ingin menyelesaikan masalah dengan n disk, kita akan membutuhkan 2ⁿ langkah. Namun, karena kita juga perlu menambahkan langkah untuk memindahkan disk terakhir dari tiang A ke tiang C, maka jumlah langkah yang dibutuhkan untuk menyelesaikan masalah ini adalah 2^n-1.

Implementasi dan Penyelesaian Permainan Menara Hanoi

Ilustrasi Permainan Menara Hanoi

Jika hanya ada satu piringan pada menara Hanoi, maka proses memindahkannya ke tiang lain sangat mudah dilakukan. Perhatikan gambar berikut:

Kita hanya melakukan satu kali perpindahan piringan. Jika menara Hanoi memiliki dua piringan, maka kita lakukan perpindahan sebagai berikut:

Perhatikan bahwa kita melakukan dua kali langkah yang sama seperti pada menara Hanoi dengan satu piringan, dan langkah terakhir memindahkan piringan terkecil di tempat teratas. Secara matematis, banyaknya langkah dapat dituliskan

2 (1)+1 =3

Jadi, kita melakukan 3 kali perpindahan.

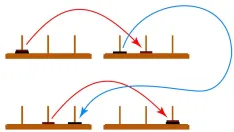
Jika menara Hanoi memiliki tiga piringan, maka cara untuk memindahkan ketiga piringan tersebut ke tiang yang lain adalah sebagai berikut

Perhatikan bahwa kita melakukan dua kali langkah yang sama seperti pada menara hanoi dengan dua piringan, dan langkah terakhir meletakkan piringan terkecil di tempat teratas, dituliskan

2 ( 2 (1) + 1) + 1 =7

Jadi kita melakukan 7 kali perpindahan.

Sekarang misalkan f(n) menyatakan langkah paling sedikit yang dibutuhkan untuk menyelesaikan menara Hanoi yang memiliki n buah piringan. Berdasarkan percobaan sebelumnya diperoleh

f (1) = 1

f (2)= 2 f (1)+1 = 2 (1) + 1=3

f (3)=2 f (2)+1 = 2 (3) + 1=7

yang mana merupakan barisan rekursif. Berapa langkah paling sedikit untuk menyelesaikan menara Hanoi yang memiliki 4 buah piringan? lebih jauh lagi, untuk n buah piringan? Tentu, kita dapat melihat polanya dengan mudah. Untuk n buah piringan maka kita punya rumus rekursif

f (1)=1 dan f (n) = 2 f (n-1) + 1 untuk n = 2,3,4.....

Belum lengkap rasanya jika tidak disertai bentuk eksplisit dari rumus rekursif tersebut. Untuk mencarinya, pandang barisan rekursif berikut

f(n)=2f(n-1)+1

2f(n-1)=2²f(n-2)+2

2²f(n-2)=2³f(n-3)+2²

:

2^n-3f(3)=2^n-2f(2)+2^n-3

2^n-2f(2)=2^n-1f(1)+2^n-2

Jumlahkan setiap baris untuk mendapatkan

f(n)=2^n-1f(1)+(1+2+2²+....+2^n-3+2^n-2)      (*)

Perhatikan bahwa 1+2+2²+....+2^n-3+2^n-2 merupakan deret geometri berhingga dengan rasio 2 yang memiliki jumlah :

Karena f(1)=1, jadi (*) dapat dituliskan sebagai

f(n)=2^n-1+2^n-1-1=2ⁿ-1

Akhirnya kita mendapatkan bentuk eksplisit dari f(n) sebagai

f(n)=2ⁿ-1, untuk n=1,2,3,...

Dari sini kita tahu bahwa langkah paling sedikit untuk menyelesaikan menara Hanoi dengan 5 piringan adalah sebanyak f(5)=2⁵-1=31 langkah. Jika kamu tertarik memainkan permainan ini secara online, silahkan klik link berikut : Bermain Menara Hanoi dengan 5 Piringan (Game hanya bisa dimainkan di PC).

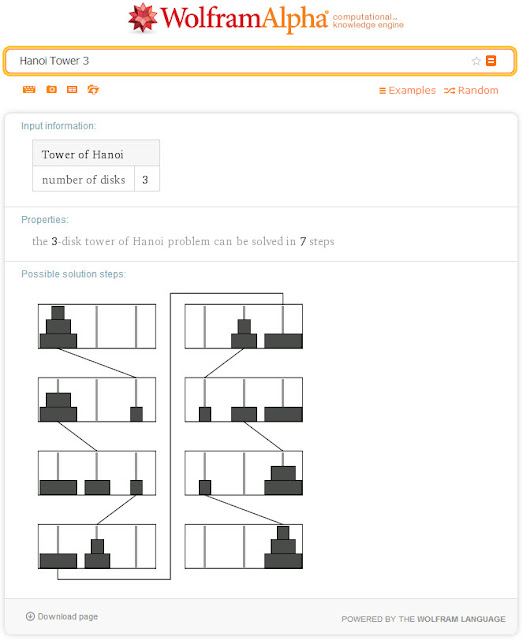
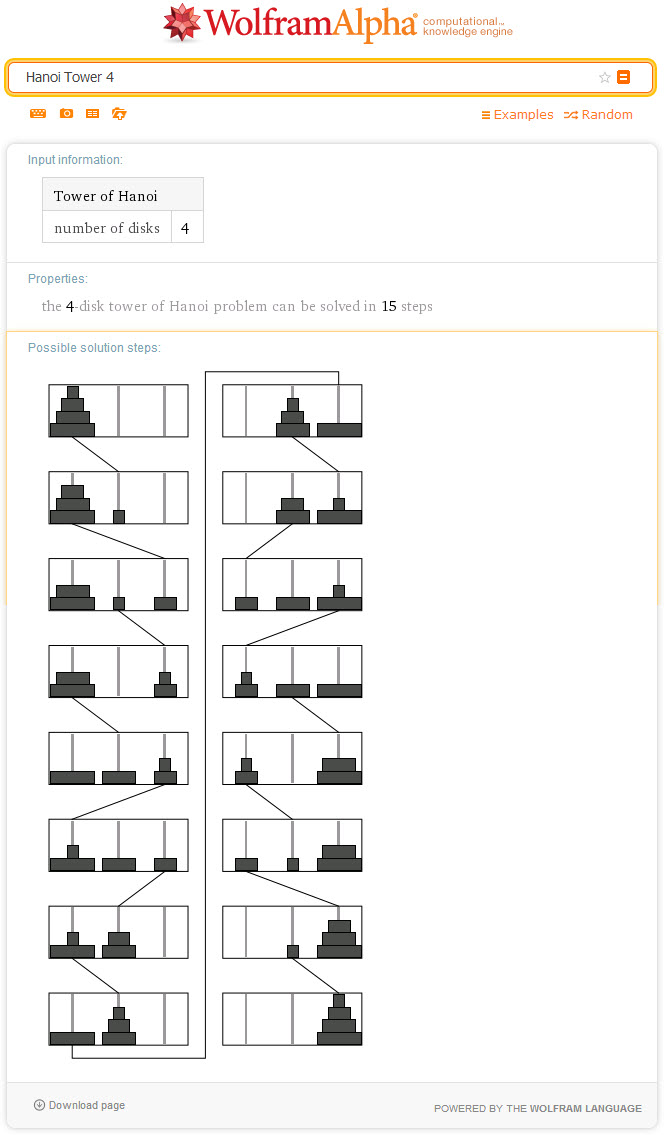
Ilustrasi gambar penyelesaian permainan menara hanoi

Penyelesaian permainan menara hanoi juga dapat dilakuan dengan cara lain, berikut ini berasal dari WolframAlpha

Kesimpulan 

Tower of Hanoi adalah sebuah permainan matematika yang sederhana namun memiliki banyak aplikasi dalam bidang komputer dan ilmu komputasi. Perhitungan matematika yang digunakan dalam permainan ini dapat dijelaskan dengan metode rekursi dan dapat diterapkan dalam algoritma pencarian, pemrograman rekursif, dan masalah yang lebih kompleks dalam ilmu komputasi.